오늘은 컴퓨터가 2의 보수 표현에 대한 일반적인 산술 방법과 연산을 처리하는 과정을 알아보겠습니다.
1. 덧셈
1) 덧셈
2의 보수로 표현된 수들 간의 덧셈 방법은 먼저 두 수를 더하고, 만약 올림수가 발생하면 버리는 것 입니다.
만약 덧셈 결과값의 부호가 1이라면, 그 값은 2의 보수로 표현된 음수를 나타냅니다.
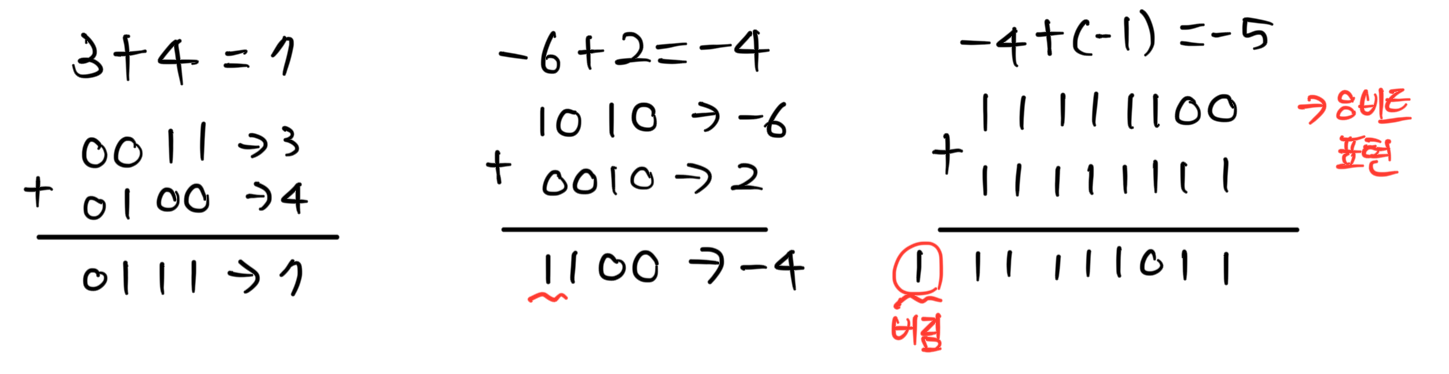
2) 병렬가산기

위의 그림은 덧셈을 수행하는 하드웨어인 병렬 가산기 입니다.
병렬 가산기는 데이트 비트 수만큼의 전가산기들로 구성됩니다. 전가산기들은 올림수 비트를 전송하는 선에 의해 연결되는데, 하위 단계의 전기산기에서 발생한 올림수가 상위 단계 전가산기의 올림수 입력으로 들어갑니다.
그림은 4비트 데이터 A와 B를 더하여 합 S를 출력하는 과정을 보여줍니다. 점선으로 표시된 부분이 병렬 가산기이며 나머지 부분은 플래그를 세트하기 위한 회로들입니다.
합의 최상위 비트는 부호 비트이므로 부호(S) 플래그로 직접 연결됩니다. 양수이면 0, 음수이면 1로 세트됩니다.
덧셈 결과에 대한 올림수(C) 플래그는 최상위 단계의 전가산기로부터 발생하는 올림수(C4)에 의해 세트됩니다.
합의 모든 비트들이 0이면, Z플래그가 1로 세트됩니다.
병렬가산기(parallel adder): 여러 비트들로 이루어진 두 개의 데이터에 대한 덧셈을 수행하는 회로로서 비트 수만큼의 전가산기(full adder)들로 구성
3) 오버플로우
덧셈과정에서 수의 표현 범위를 초과하는 경우에는 전혀 틀린 결과를 산출하게 됩니다. 이것을 오버플로우라고 합니다.
오버플로우(overflow): 2의 보수들 간의 덧셈 결과값이 표현 범위를 초과하는 경우에 발생하는 오류
예시를 들어보겠습니다.

표현 범위를 초과하기 때문에 잘못된 값이 나오고 있습니다.
덧셈과정에서의 오버플로우(V)는 올림수들 간의 exclusive-OR 연산을 통해 검출할 수 있습니다.
V = C4 ⊕ C3
V 플래그는 1로 세트되며, CPU는 그 결과값이 다른 연산에 사용되지 않도록 적절한 조치를 취해야 합니다.
2. 뺄셈
뺄셈은 덧셈을 이용하여 수행됩니다.
A(피감수)로부터 B(감수)를 빼려면, B를 음수화 한 다음에 A와 더하면 됩니다.
A - (+B) = A + (-B)
A - (-B) = A + (+B)
일반적으로 ALU에 뺄셈을 위한 회로를 별도로 두지 않고 가산기를 이용하여 뺄셈을 수행합니다.

위의 회로에서 A레지스터로 부터 들어오는 수는 병렬 가산기로 직접 입력되고, B레지스터로 들어오는 수는 보수기를 통해 병렬 가산기로 들어옵니다. 보수기로는 제어신호가 가해지는데, 덧셈인 경우에는 0이 입력되고 뺄셈인 경우에는 1이 입력되어 2의 보수로 변환된 다음 가산기에 입력됩니다.
보수기(complementer): 입력 데이터에 대하여 보수 연산을 수행하는 회로 모듈
뺄셈에서의 오버플로우도 덧셈과 같은 회로를 통해 검출할 수 있습니다.
3. 곱셈
1) 부호 없는 정수에 대한 곱셈

위의 식은 2진수 곱셈 13 * 11을 나타내고 있습니다.
두개의 n-비트 정수들을 곱하면, 결과값의 길이는 최대 2n 비트가 됩니다.
식에서는 마지막 단계에서 모든 부분 적들을 더하여 최종 결과를 구하는것으로 표시합니다.
하지만 이 계산을 컴퓨터에서 수행할 때는 부분적이 발생할때마다 합을 계산함으로써, 중간 결과인 부분적을 저장해 두기 위한 레지스터를 별도로 사용하지 않도록 하고 있습니다. 검사하는 승수의 비트가 1이면 덧셈과 시프트를 수행하지만, 0인 경우에는 시프트만 하기 때문에 처리시간을 단축할 수 있습니다.

위 그림은 곱셈기 구성에 대해 나타내고 있습니다. 중앙에는 병렬 가산기가 위치하고, 그 입력들은 피승수가 저장되어 있는 M레지스터와 A레지스터로 부터 들어옵니다. 덧셈 과정에서 발생한 올림수는 C플래그에 저장됩니다.
C플래그 - A레지스터 - Q레지스터가 직렬로 연결되어 시프트 연산을 수행할 수 있도록 합니다.

13 * 11 과정을 표를 통해 알아보겠습니다.
- 초기상태: M에 1101, Q에 1011을 세트합니다. A레지스터의 모든 비트들과 C를 0으로 초기화 합니다.
- 단계 1
1) Q의 최하위 비트인 Q0의 값이 1이므로 A <- A+M을 수행합니다.
2) 우측 시프트를 수행합니다. - 단계 2
1) Q0 = 1이므로 A <- A+M을 수행합니다.
2) 우측 시프트를 수행합니다. - 단계 3
1) Q0 = 0 이므로 연산을 수행하지 않습니다.
2) 우측 시프트를 수행합니다. - 단계 4
1) Q0 = 1 이므로 A <- A+M을 수행합니다.
2) 우측 시프트를 수행합니다.
A-Q 레지스터에 결과값인 1000 1111이 각각 저장되어 있습니다.
2) 2의 보수간에 곱셈, Booth 알고리즘
2의 보수들 간의 곱셈에는 Booth 알고리즘이 가장 널리 사용되고 있습니다.
알고리즘의 흐름도는 다음과 같습니다.

부호없는 곱셈기의 구성도에서 다음과 같은 것들을 추가하면됩니다.
- M 레지스터의 병렬 가산기 사이에 보수기를 추가
- Q레지스터의 우측에 Q-1이라고 부르는 1-비트 레지스터를 추가, 출력이 Q0와 함께 제어회로로 입력되도록 함
제어회로는 승수의 비트들을 검사할때, Q0뿐만이 아니라 Q-1도 함께 검사합니다.
두 비트의 값이 같으면 우측 시프트만 수행하고 값이 다르면 연산을 수행합니다.
Booth 알고리즘을 활용한 -7 * 3 계산을 표로 확인해보겠습니다.

- 초기상태: M = 1001, Q = 0011, Q-1 =0, 계수 = 4 세트
- 단계 1
1) Q0Q-1 = 10 이므로 A <- A-M
2) 우측 시프트
3) 계수 -1, 계수 = 3 - 단계 2
1) Q0Q-1 = 11, 즉 두 값이 같으므로 연산 수행 X
2) 우측 시프트,
3) 계수 -1, 계수 = 2 - 단계 3
1) Q0Q-1 = 01 이므로 A <- A+M
2) 우측 시프트, 값이 음수이므로 1로 채움
3) 계수 - 1, 계수 = 1 - 단계 4
1) Q0Q-1 = 00, 연산수행 X
2) 우측 시프트, 값이 음수이므로 1로 채움
3) 계수 -1, 계수 = 0 => 연산 종료
4. 나눗셈
나눗셈은 곱셈보다 다소 더 복잡하지만 같은 원리에 근거를 두고 있습니다.
나눗셈도 반복적인 시프트와 덧셈 또는 뺄셈으로 이루어집니다.
곱셈과 마찬가지로 먼저 식을 보겠습니다.

피제수 10010011을 제수 1011로 나누는 과정을 보여주고 있습니다.
좌측에서 부터 우측으로 검사하며 제수가 피제수를 나눌 수 있게 될 때까지 이동하면서 검사합니다.
그렇게 될 때 까지 몫은 0을 채워나갑니다.

위의 그림은 부호없는 나눗셈 알고리즘의 흐름도 입니다. 위의 알고리즘을 약간 수정하면 부호가 음수인 경우에도 적용할 수 있습니다.
(+7) / (-3) 연산을 표로 나타내 보겠습니다.

- 초기단계: A = 0000, Q = 1111, M = 1101 세트
- 단계 1
1) 좌측 시프트
2) A와 M의 부호가 다르므로 A <- A+M
3) A의 부호가 바뀌었으므로 Q0= 0 세트, 원래 값으로 복원 - 단계 2
1) 좌측 시프트
2) A와 M의 부호가 서로 다르므로 A <- A+M
3) A의 부호가 바뀌었으므로 Q0=0 세트, 원래 값으로 복원 - 단계 3
1) 좌측 시프트
2) A와 M의 부호가 다르므로 A <- A+M
3) A = 0이므로 유지, Q0 = 1 세트 - 단계 4
1) 좌측 시프트
2) A와 M의 부호가 서로 다르므로 A <- A+M
3) A의 부호가 바뀌었으므로 Q0 = 0 세트, 원래 값으로 복원
해당 과정을 거쳤을 때 나머지는 A 레지스터의 내용인 0001(+1) 몫은 Q레지스터의 값인 0010의 보수 1110(-2)이 됩니다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] 제어유니트(Control Unit)와 마이크로프로그램 (0) | 2025.04.27 |
|---|---|
| [컴퓨터 구조] 부동소수점 수의 표현과 산술연산 (0) | 2025.04.22 |
| [컴퓨터 구조] 시프트 연산 (0) | 2025.04.15 |
| [컴퓨터 구조] 논리연산 (0) | 2025.04.10 |
| [컴퓨터 구조] 산술논리연산장치(ALU)의 구성요소와 정수의 표현 (0) | 2025.04.09 |